Apêndice 06 - Memorial de cálculo de elementos do projeto

Histórico de Versões

Data	Responsável(eis)	Descrição	Versão
29/04/2024	Tiago e Débora	Desenvolvimento de memorial de cálculo	1.0
04/05/2024	Débora	Revisão	1.1
04/05/2024	Tiago e Débora	Revisão e carregamento das imagens	1.2

Introdução

Neste apêndice, será apresentado o memorial de cálculo utilizado para dimensionar os componentes de energia essenciais ao projeto em questão. Dessa forma, os cálculos fundamentais foram realizados para determinar as especificações necessárias dos componentes elétricos, como motores, seu rendimento e potência mecânica, como também o balanço de energia do volume de controle em questão e a transferência de calor, garantindo um dimensionamento preciso e eficiente. Através desses cálculos, é possível assegurar que os componentes selecionados atendam às demandas de energia do sistema, proporcionando um funcionamento adequado e otimizado. Este documento servirá como guia para o desenvolvimento e implementação do projeto, garantindo sua viabilidade e eficácia no fornecimento de energia.

Motor

O motor síncrono de corrente alternada monofásico, peça central do projeto, é composto por dois elementos fundamentais: o rotor e o estator. No rotor, encontra-se o enrolamento por onde flui corrente contínua, responsável por gerar um fluxo magnético constante, denominado enrolamento de campo. Este fluxo é essencial para a operação do motor. Por outro lado, o estator abriga um conjunto de bobinas ou enrolamentos, neste caso, monofásicos, por onde flui corrente alternada. Essas correntes alternadas geram grandezas magnéticas variáveis, que interagem com o campo magnético do rotor para gerar o movimento necessário. Além disso, o motor é descrito por um circuito equivalente de armadura, que representa o estator e suas características elétricas relevantes para os cálculos e análises de desempenho (D. Umans, 2014).

Figura 1: Circuito equivalente de armadura (estator).

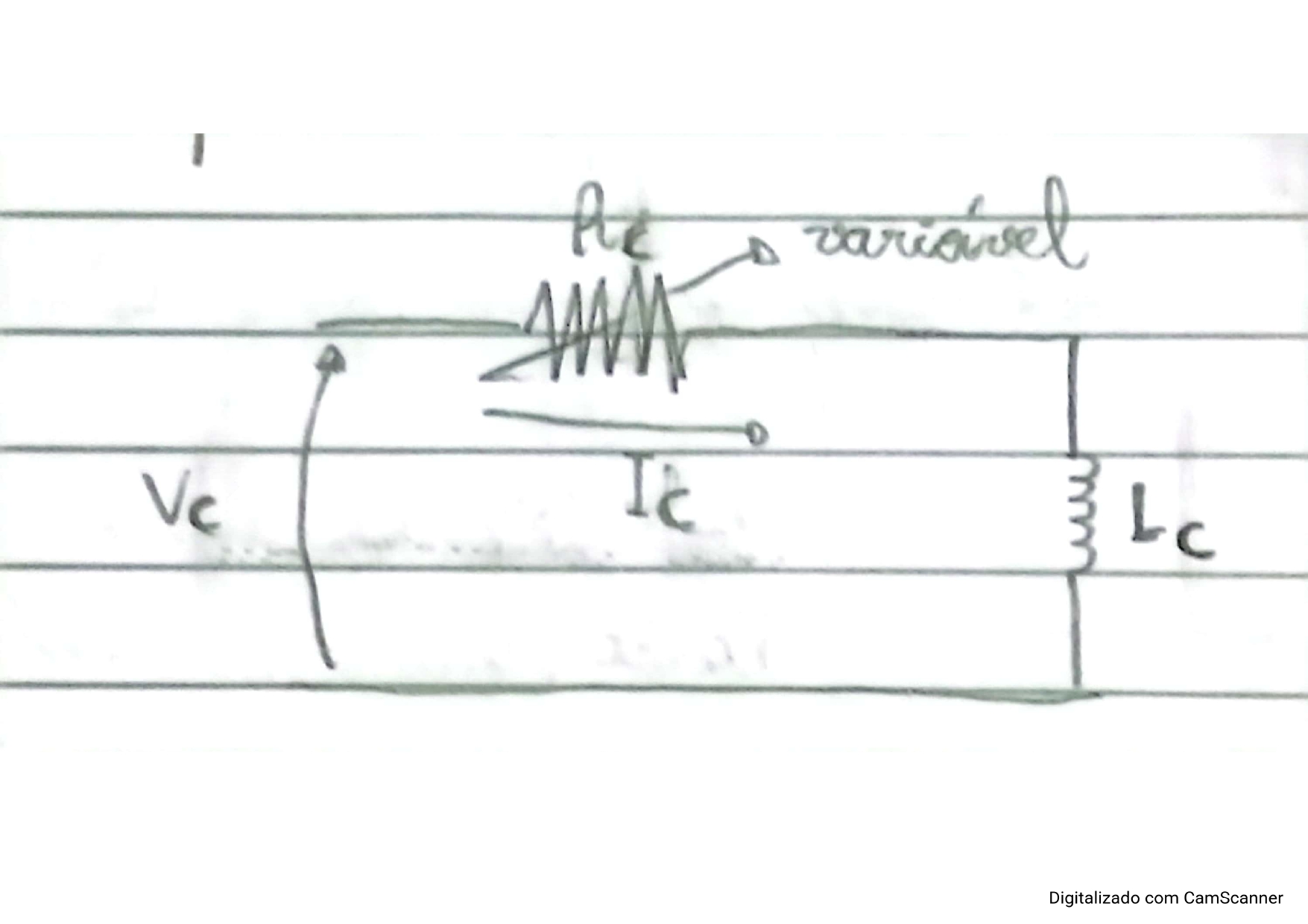
Fonte: Autor

Êa: Tensão da armadura
Vt: Tensão terminal
Îa: Corrente de armadura
Xs: Resistência síncrona
Ra: Resistência de armadura

Usando a lei de malha:

$$ \widehat{E}_a = \widehat{V}_t-(R_a+JX_s)\widehat{I}_a \ \ \ \ \ (Eq. 1)$$

Estator - enrolamentos monofásicos de corrente alternada

Figura 2: Representação do circuito de campo (rotor).

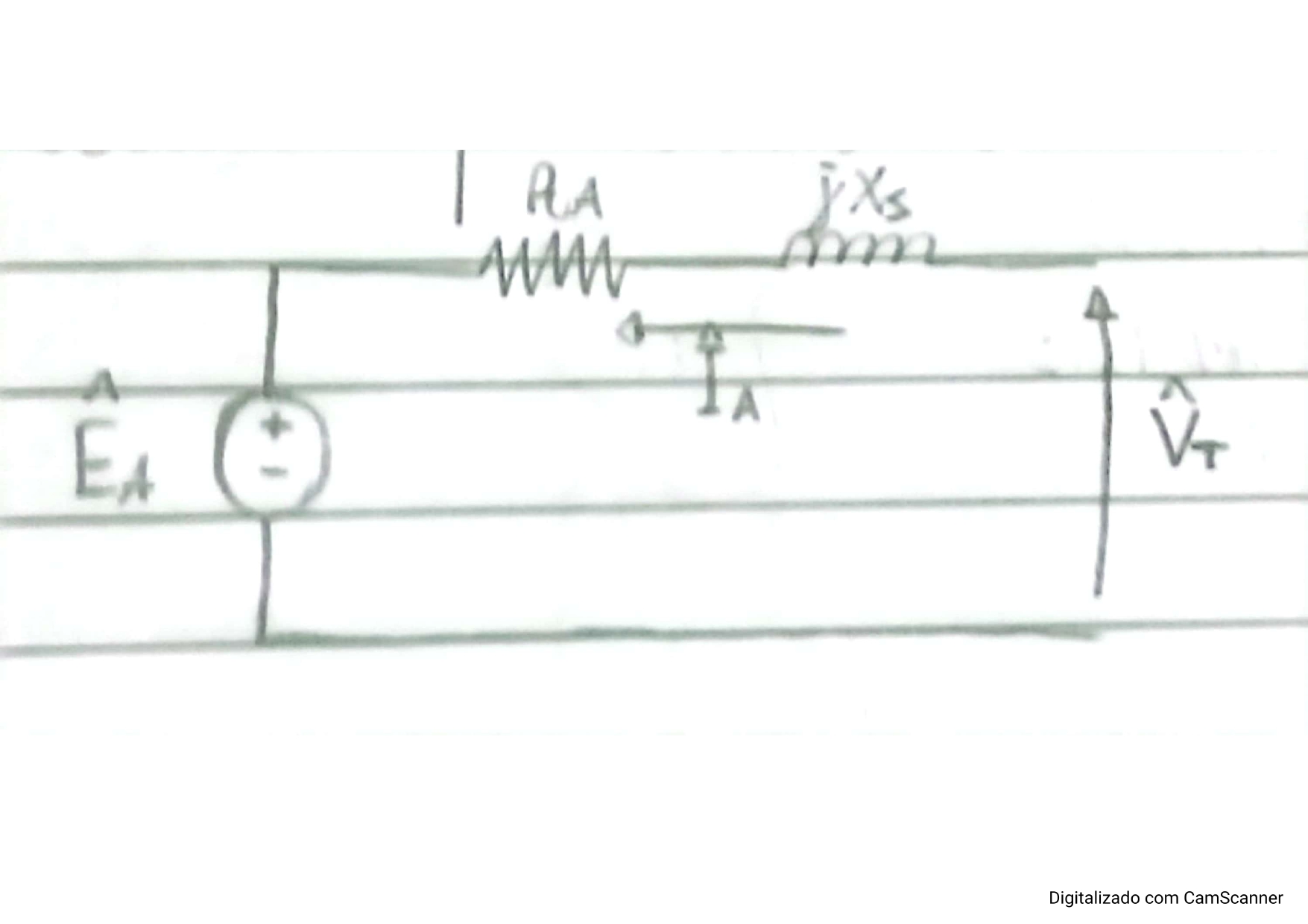
Fonte: Autor

Rc: Resistência variável de campo
Ic: Corrente de campo Lc: Indutância de campo Vc: Tensão de campo

\[ E_a= K\phi\omega \ \ \ \ \ (Eq.2) \]

K: Fator de enrolamento
\(\delta\): Frequência angular \(\Phi\): Fluxo magnético

Esta equação relaciona circuito de campo com o circuito de armadura, onde o fluxo magnético é uma função da corrente de campo

\[ \Phi = f(I_c) \ \ \ \ \ (Eq. 3) \]

Especificações térmicas do fabricante - Tensão de alimentação (\(\widehat{V}_t\)) 220 - 240v - Frequência de operação: 50/60 Hz (valor dependente da frequência da rede) - Corrente a vazio: 0,25A
- Potência a vazio: 55W
- Rodação a vazio (\(\omega\)): 3800 rpm

Teste com ventilador acoplado como carga

• Corrente em carga (\(\widehat{I}_a\)): 0,75A \(\pm\) 10%
• Potência em carga: 165W \(\pm\) 10 %
• Rotação da carga 13.000 rpm \(\pm\) 10 %
• Torque do motor (\(\tau\)): \(99,48.10^{-3}\) N/m

O erro de 10% é adivindo das grandezas em carga, e se deve às perdas de energia no rotor e no estator.

• Perdas no rotor: perdas por atrito e ventilação; Perdas no núcleo magnético
• Perdas na estator: perdas de energia por calor devido a efeito Joule A partir da potência em carga, podemos estimar a potência de eixo do motor:

\[ P_m = \frac{P_{mec}}{\eta.cos\theta} \ \ \ \ \ (Eq. 4) \]

\[ P_{mec} = P_{m}\eta.cos\theta \ \ \ \ \ (Eq. 5) \]

\(P_m\): Potência em carga \(P_{mec}\): Potência mecânica \(N\): Eficiência do motor \(cos\): Fator de potência do motor

Porém como não se tem o fator de potência da máquina, é possível calcular sua potência mecânica a partir do torque (D. Umans, 2014):

\[ P_{mec}=\tau .2\pi\frac{N}{60} \ \ \ \ \ (Eq. 6) \]

\[ P_{mec}=99,48.10^{-3}\pi\frac{13000}{60} [ N.m.Hz = \frac{N.m}{s}]\]

\[ P_{mec}= 135,42W \]

Calcula-se também o rendimento do motor através da sua potência elétrica e potência mecânica:

\[ \eta = \frac{P_{mec}}{Pm}= 82,072 \ \ \ \ \ (Eq. 7)\]

Cálculo da vazão de ar do Volume de Controle

Para este cálculo, serão deduzidas equações e princípios para a área de interesse, dessa forma o volume de controle (VC).

Figura 3: Diagrama do volume de controle 1 de interesse.

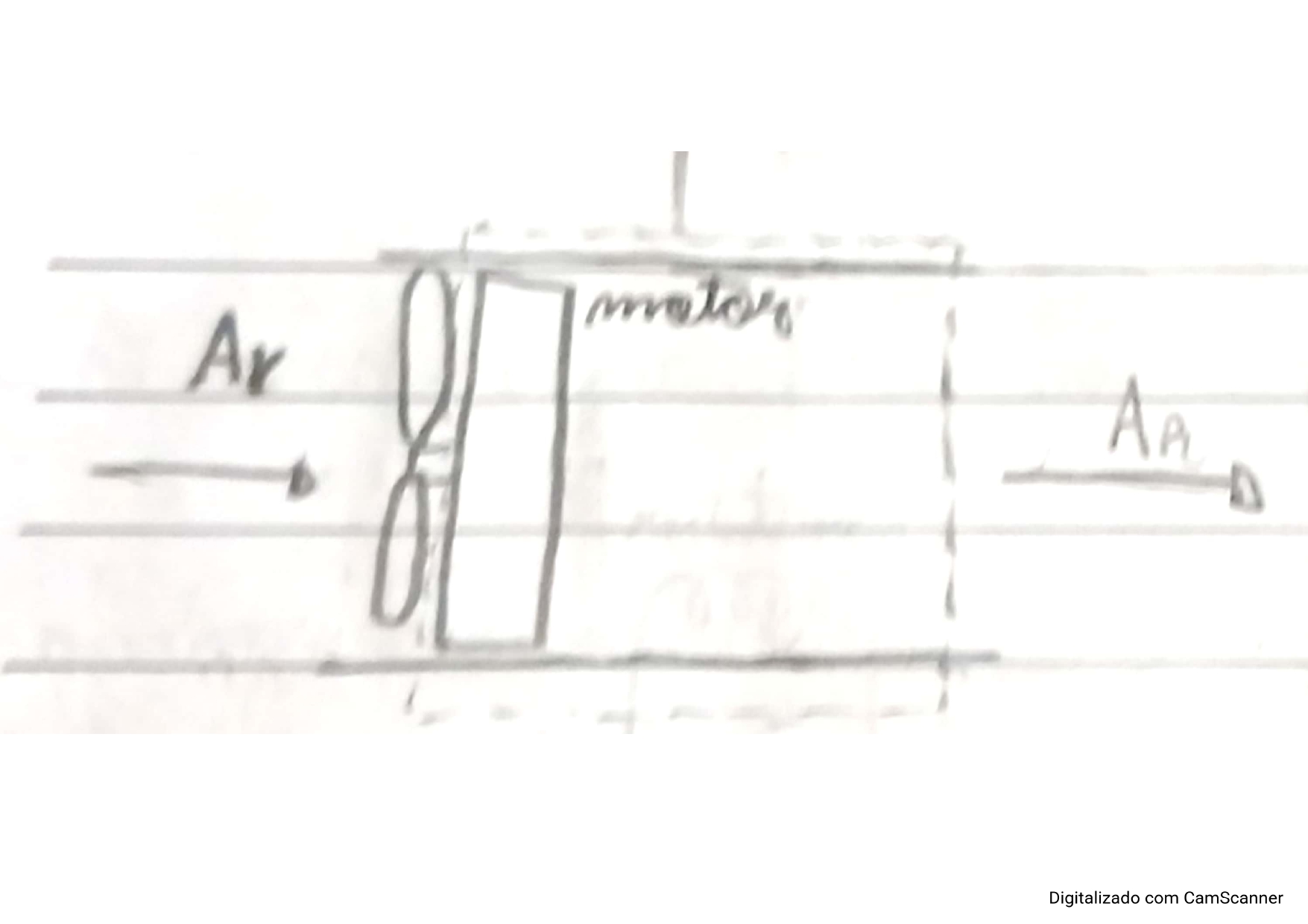
Fonte: Autor

Considera-se uma entrada e uma saída e um trabalho de eixo advindo do motor

Princípio da conservação de massa para um Volume de Controle

O princípio da conservação de massa para um VC diz que a taxa de variação de massa contida no interior do volume de controle no instante deve ser igual a taxa de escoamento da massa através da entrada do VC no instante \(t\) (J. Moran et al., 2005).

\[ \frac{d_{mVC}}{dt}=\dot{m}_e-\dot{m}s \left [ kg/s\right ] \ \ \ \ \ (Eq. 8) \]

Considerando um escoamento unidimensional, deduz-se as condições:

• O fluxo de ar será normal à fronteira do VC na entrada e na saída

• Todas as propriedades intensivas, incluindo a velocidade e o volume específico são uniformes com a posição (valores médios globais) sobre a área de entrada ou saída através da qual a matéria escoa

Figura 4: Diagrama de escoamento unidimensional.

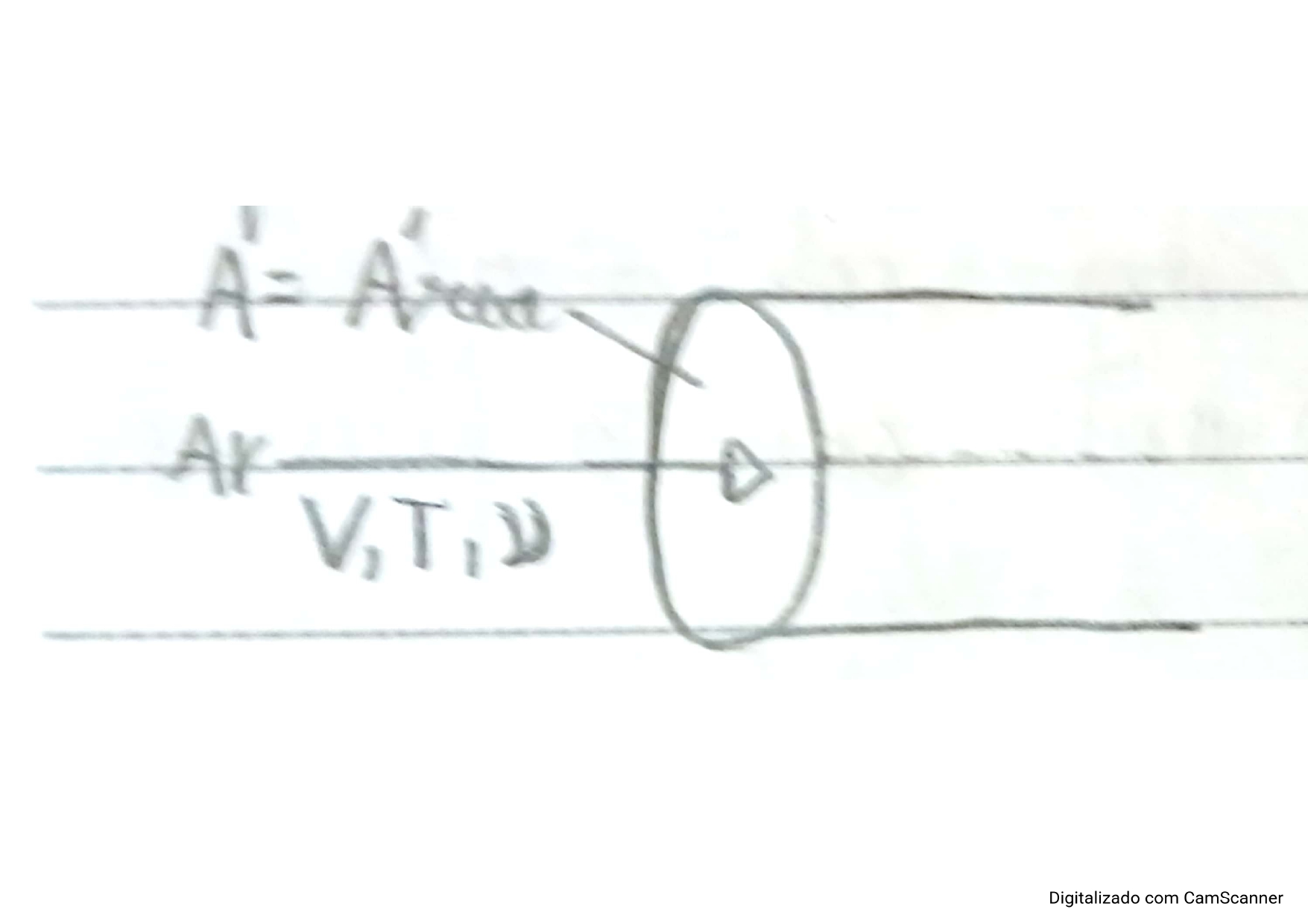
Fonte: Autor

\(V\): velocidade
\(t\): temperatura
\(\upsilon\): volume específicos

Em base dessas suposições a taxa de massa pode ser calculada por meio da seguinte equação:

\[\dot{m}=\frac{A.V}{\upsilon} \ \ \ \ \ (Eq. 9) \]

\[ \upsilon =\rho.A.V \left [ Kg/s \right ] \ \ \ \ \ (Eq. 10) \]

A taxa volumétrica é o produto da área e da velocidade:

\[Q = A.V \left [ m^3/s \right ] \ \ \ \ \ (Eq. 11)\]

\(Q\): Taxa volumétrica

Neste estudo, serão considerados os parâmetros e propriedades em regime permanente, ou seja, as propriedades não se alteraram ao longo do tempo assim temos que:

\[ \frac{d_{mVC}}{dt}=0 \ \ \ \ \ (Eq. 12) \]

E a equação de Balanço de massa ficará da seguinte maneira:

\[ \dot{m_e}-\dot{ms}=0 \]

\[ \dot{m_e}=\dot{ms} \]

\[ \rho.A_e.V_e=\rho.A_s.V_s \ \ \ \ \ (Eq. 13) \]

Assim as taxas totais de entrada e saída de massa são iguais.

Princípio da conservação de energia para um Volume de Controle

O Balanço da taxa de energia para VC pode ser obtido modificando-se o balanço da taxa de energia para sistema fechado, de forma a levar em conta as transferências de energia para o VC justamente com o fluxo de massa.

Assim o princípio de conservação de energia estabelece que a taxa temporal de variação de energia no interior do volume de controle no instante \(t\) será igual a: Taxa Líquida no qual a energia está sendo transferida para seu interior por transferência de calor no instante \(t\); subtraído da Taxa Líquida na qual a energia está sendo transferida para fora por trabalho no instante \(t\); somado a Taxa Líquida de energia transferida para o volume de controle juntamente com o fluxo de massa (J. Moran et al., 2005). Dessa forma:

\[\frac{dE_{VC}}{dt}=\dot{Q}-\dot{W}+\dot{m_s}.\varrho_{s}-\dot{m_e}.\varrho_{e} \ \ \ \ \ (Eq.\ \ 14)\]

\(\varrho\) seriam todas as taxas de energia interna, cinética e potencial, assim:

\[\dot{m}.\varrho=\dot{m}(u+\frac{V^2}{2}+gz) \ \ \ \ \ (Eq.\ \ 15)\]

\(u\): energia interna; \(g\): gravidade; \(z\): altura.

A transferência de energia através da Fronteira do volume de controle pode ocorrer por trabalho.

O trabalho \(\dot{W}\) será avaliado da seguinte maneira:

Trabalho associado à pressão do fluido à medida que a massa é introduzida nas entradas e removida na saída. Designada por \(\dot{W}_{VC}\), que inclui todos os outros efeitos devido ao trabalho, como aqueles associados a eixos que giram, o deslocamento de fronteiras e de efeitos elétricos;

A taxa de transferência de energia por meio de trabalho é dada por:

\[ \dot{W}=\overrightarrow{F}.\overrightarrow{V} \ \ \ \ \ (Eq.\ \ 16) \]

\(\overrightarrow{F}\): Vetor força; \(\overrightarrow{V}\): Vetor velocidade

Já o trabalho associado à pressão da matéria escoando através de uma saída s:

\[ \dot{W}=F_s.V_s \ \ \ \ \ (Eq.\ \ 17) \]

\[ F_s=p_s.A_s \ \ \ \ \ (Eq.\ \ 18) \]

\[ \dot{W}=(p_s.A_s).V_s \ \ \ \ \ (Eq.\ \ 19) \]

\(p\): pressão

Dessa maneira o termo de trabalho \(\dot{W}\) da equação da conservação de energia será:

\[ \dot{W}=\dot{W}_{VC}+(p_s.A_s).V_s -(p_s.A_s).V_e \ \ \ \ \ (Eq.\ \ 20) \]

sendo:

\[ \dot{m}= \frac{A.V}{\upsilon}\rightarrow A.V=\dot{m}.\upsilon \]

\[ \dot{W}=\dot{W}_{VC}+(p_s.A_s).V_s -(p_s.A_s).V_e \ \ \ \ \ (Eq.\ \ 21) \]

Substituí-se esta equação na equação do balanço da taxa de energia para VC, tem-se:

\[ \frac{dE_{VC}}{dt}=\dot{Q}_{VC}-\dot{W}_{VC}+\dot{m_s}(u+p_s.v_s.\frac{V^2_s}{2}+gz_s)-\dot{m_e}(u+p_e.\upsilon_e.\frac{V^2_e}{2}+gz_e) \ \ \ \ \ (Eq.\ \ 22) \]

Sabendo que a entalpia específica é dada por:

\[ h=u+p.\nu \ \ \ \ \ (Eq.\ \ 23) \]

O Balanço de energia será:

\[ \frac{dE_{VC}}{dt}=\dot{Q}_{VC}-\dot{W}_{VC}+\dot{m_s}.(h_s. \frac{V^2_s}{2}+gz_s)-\dot{m_e}(h_e. \frac{V^2_e}{2}+gz_e) \ \ \ \ \ (Eq.\ \ 24) \]

Já a taxa de transferência de calor gerada pela resistência será dada pela equação da taxa de calor específico do ar:

\[ \dot{Q}_{sai}=\dot{m}.C_p(T_s-T_e) \ \ \ \ \ (Eq.\ \ 25) \]

\(T_s\): Tempo de saída
\(T_e\): Tempo de entrada
\(Cp\): Calor específico

Para este caso, tem-se um escoamento interno do ar por toda a tubulação, e este ar será submetido a um aquecimento externo por meio de resistores. Será calculada a taxa de transferência de calor para condutor interno (A. Çengel; J. Ghajar, 2012):

\[ \dot{Q}=h.A_s.\Delta T = c_p.\dot{m}.(T_s-T_e) \ \ \ \ \ (Eq.\ \ 26) \]

Tranferencia de Calor

Será considerado os números de Nusselt, Prandt e Reynolds para descobrir o coeficiente de convecção térmica e determinar a temperatura de superfície do condutor.

O número de Prandtl expressa a relação entre a difusão molecular de quantidade de movimento e a difusão molecular térmica dentro do próprio fluido (A. Çengel; J. Ghajar, 2012). Logo, este número representa a medida de eficiência entre a difusividade de movimento e a difusividade térmica. Sendo matematicamente escrita como:

\[ P_r=\frac{\upsilon }{\alpha} \ \ \ \ \ (Eq.\ \ 27) \]

Vale ressaltar que a equação acima foi obtida através da equação do balanço de energia aplicada para um fluido.

Número de Nusselt

É definido como a forma adimensional do coeficiente convectivo de troca de calor h (A. Çengel; J. Ghajar, 2012), e é definido como:

\[ Nu=\frac{q_{conv}}{q_{cond}}= \frac{h.\Delta T }{k.\frac{\Delta T}{L}}=\frac{h.L}{k} \ \ \ \ \ (Eq.\ \ 28) \]

Número de Reynolds

Número usado para caracterizar o regime do escoamento (A. Çengel; J. Ghajar, 2012). E o número é matematicamente definido como:

\[ R_e=\frac{\rho.V.D}{\mu }=\frac{V.D}{v} \ \ \ \ \ (Eq.\ \ 29) \]

E esta equação do número de Reynolds foi obtida através da equação da quantidade de movimento. Tem-se as seguintes deduções feitas com o número de Reynolds para o caso de convecção interna forçada dentro de um cilindro (considerando sua base uma placa plana):

• Para \(R_e < 5.10^5\) , teremos um escoamento laminar;

• Para \(5.10^5 < R_e < 1.10^7\), teremos um escoamento turbulento.

Cálculo do coeficiente convectivo a partir da equação de energia.

Este cálculo é caracterizado por um escoamento laminar de um fluido sobre uma placa plana, e foi feito por Blasius. Considerando que o coeficiente convectivo é obtido igualando o fluxo de calor por condução e convecção, chegará na seguinte fórmula:

\[ h=\frac{-k.\frac{\partial T}{\partial x}_{y=0}}{T_s-T_{\infty}} \ \ \ \ \ (Eq.\ \ 30) \]

Neste problema, Blasius considerou um escoamento como sendo bidimensional, em regime permanente e com Número de Prandtl unitário. A partir disso, foram definidas as equações e condições de contorno para o problema (A. Çengel; J. Ghajar, 2012).

• Conservação de massa:

\[ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial x}= 0 \ \ \ \ \ (Eq.\ \ 31) \]

• Conservação da quantidade de movimento:

\[ u\frac{\partial u}{\partial x}+v\frac{\partial v}{\partial y}=\alpha \frac{\partial^2 T}{\partial y^2} \ \ \ \ \ (Eq.\ \ 32) \]

• Conservação da energia:

\[ u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}=\alpha \frac{\partial^2 T}{\partial y^2} \ \ \ \ \ (Eq.\ \ 33) \]

• Condições de contorno:

\[ Em \ x=0: u(0,y) = V; T(0,y)=T_{\infty} \]

\[ Em \ y=0: u(x,0)=0; T(x,0)=T _1; v(X,0)=0 \]

\[ Em \ y\rightarrow \infty: u(x, \infty); T(x, \infty)=T_{\infty} \ \ \ \ \ (Eq.\ \ 34) \]

A solução proposta por Blasius foi transformar as equações de conservação de massa e de conservação da quantidade de movimento em uma única equação ordinária pela adição de uma variável adimensional de similaridade \(\eta\):

\[ y=\sqrt{\frac{V}{vx}} \ \ \ \ \ \ \ \ \ \ (Eq.\ \ 35) \]

Introduzindo a função de corrente \(\varphi\) para a velocidade:

\[ u = \frac{\partial \varphi }{\partial x} \ \ \ \ \ (Eq.\ \ 36) \]

\[ v=-\frac{\partial \varphi }{\partial x} \ \ \ \ \ (Eq.\ \ 37) \]

De tal forma que a equação da conservação de massa seja totalmente satisfeita e eliminada.

Depois definiu-se uma função de similaridade:

\[ f(x)= \frac{\varphi }{V\sqrt{\frac{v.x}{V}}} \ \ \ \ \ (Eq.\ \ 38) \]

A partir disso, é possível manipular as componentes de velocidade e derivá-las. E utilizando-se das condições de contorno definidas, será possivel obter uma aproximação para a derivada de temperatura em relação a x. Portanto, Blasius chegou em uma aproximação para o coeficiente local de convecção (relacionado a uma posição x específica) (A. Çengel; J. Ghajar, 2012):

\[ h_x=0,322.P_r^{\frac{1}{3}}.k\sqrt{\frac{V}{v.x}} \ \ \ \ \ (Eq.\ \ 39) \]

Assim, o número de Nusselt local será:

\[ Nu_x=0,322.P_r^{\frac{1}{3}}.Re_{x}^\frac{1}{2}; P_r >0,6 \ \ \ \ \ (Eq.\ \ 40) \]

Depois, para calcular um número médio de Nusselt para a placa plana inteira, ao invés de em apenas um ponto x específico, somamos cada Nusselt local para todo o comprimento L da placa:

\[ Nu = \frac{1}{L}\int_{0}^{L}Nu_x.dx \ \ \ \ \ (Eq.\ \ 41) \]

E o número de Nusselt global obtido por Blasius, para este caso em específico, foi:

\[ Nu=\frac{h.L}{k}=0,664.P_r^{\frac{1}{3}}.Re_{x}^\frac{1}{2}; P_r >0,6 \ \ \ \ \ (Eq.\ \ 42) \\ e \\ Re_L<5.10^5 \]

Aonde a condutividade térmica k é avaliada sobre uma temperatura média:

\[ T_m=\frac{T_s+T_{\infty}}{2} \ \ \ \ \ (Eq.\ \ 43) \]

Nusselt de referência

O número de Nusselt de referência será representado por \(Nu_f\), que é o Nusselt que será utilizado para os cálculos do coeficiente convectivo

\[ Nu=0,023.Re^{0,8}.Pr^{1/3} \ \ \ \ \ (Eq.\ \ 44) \]

A fórmula acima foi obtida experimentalmente para o caso de um escoamento dentro de um cilindro circular.

Equação de Bernoulli

Pode-se determinar também a equação de Bernoulli, já que será feito uso de um bocal. Para utilizar-se essa equação no bocal, é necessário que o escoamento esteja em regime permanente e haja ausência de atrito e o escoamento seja incompreensível (J. Moran et al., 2005).

\[ \frac{p}{\rho }+\frac{V^2}{2}+gz=cte \ \ \ \ \ (Eq.\ \ 45) \]

Análise da bomba utilizada

Neste caso, será considerada também uma entrada meridional, onde o ângulo relativo ao deslocamento do fluido será 90º, ou seja, consideramos todo o fluido entrando normal à entrada.

Para esta bomba radial, ela possui pás voltadas para frente. Essa configuração possui uma transferência de energia maior para energia cinética do fluido e menor para energia potencial. Dessa maneira, seu objetivo primordial é fornecer mais velocidade ao fluido (Saravanamuttoo et al., 2017).

Como é conhecido o ângulo de pá (\(\beta\)), o ângulo do fluido (\(\alpha\)) e a velocidade tangencial (a partir do raio da bomba), montou-se o triângulo de velocidade na saída:

Figura 5: Triângulo de velocidade na saída do motor.

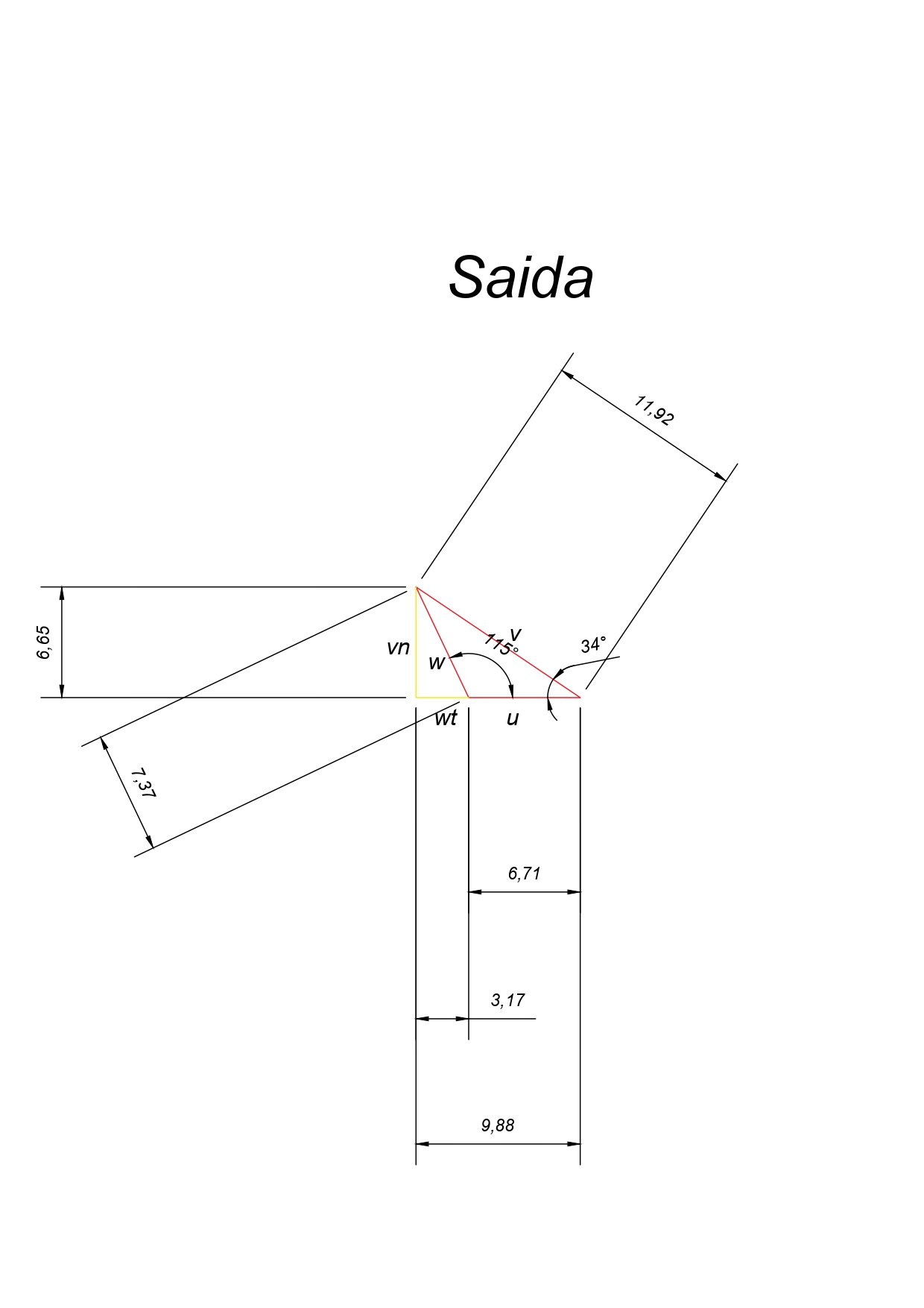
Fonte: Autor (Feito no AutoCAD 2024)

Sabe-se também que a área de passagem de uma máquina radial é dada por:

\[ A_p=\pi .D.d \ \ \ \ \ (Eq.\ \ 46) \]

\(D\): Diamêtro motor \(d\): Largura da pá

Ao se aplicar o Balanço de energia em regime permanente, desconsiderando transferência de calor e substituindo entalpia:

\[ \dot{W}=\dot{m}\left [ (u_2-u_1)+\frac{(v_2^2-v_1^2)}{2} +g(z2-z1)+\frac{p_2-p_1}{\rho })\right ] \ \ \ \ \ (Eq.\ \ 47) \]

Desconsiderando-se a energia genética potencial interna teremos:

\[ \dot{W}_{eixo}=\dot{m}(\frac{p_2-p_1}{\rho })=\dot{m}.\frac{\Delta p}{\rho} \ \ \ \ \ (Eq.\ \ 48) \]

Outra variável adivinda do trabalho e taxa mássica é salto energético, que varia a energia que a bomba está disponibilizando no fluido:

\[ Y_\infty=\frac{\dot{W}}{\dot{m}}=\frac{\Delta p}{\rho } \ \ \ \ \ (Eq.\ \ 49) \]

É possível reescrever o salto energético em função das velocidades componentes da absoluta e tangencial:

\[ Y_\infty=u_2.v_{t2}-u_1.v_{t1} \ \ \ \ \ (Eq.\ \ 50) \]

Como está sendo considerada uma entrada meridional, a componente da velocidade absoluta é zero, assim:

\[ Y_\infty=u_2.v_{t2} \ \ \ \ \ (Eq.\ \ 51) \]

Os cálculos realizados forneceram uma base sólida para o dimensionamento preciso dos componentes de energia essenciais, assegurando que atendam às demandas específicas do sistema. Com essa fundamentação, o próximo passo será implementação prática das soluções propostas.

Cálculos de parâmetros do fluido para o soprador de ar

Para os parâmetros base destes cálculos, foi primeiro feita uma aproximação da velocidade a partir dos ângulos de pá do soprador de ar, de forma manual. Depois, com um anemômetro foi obtida a velocidade real do fluido, considerando o direcionamento dado por um difusor na entrada do fluido e porteriormente um bocal para a saída do mesmo.

O difusor é utilizado para aumentar a pressão do fluido, e o bocal para diminuir esta pressão ao final do escoamento e aumentar a velocidade , gerando uma diferença de pressão e forçando o fluido a percorrer um caminho único e direcionado.

O anemômetro indicou aproximadamente 11,12 m/s, valor superior ao calculado de forma manual (6,65 m/s) devido ao uso do bocal, que devido a diferença das áreas gera uma diferença de pressão e modifica o gradiente de velocidade, e demais erros aleatórios e de instrumento, visto que a primeira velocidade foi aproximada por régua e transferidor. Sabendo a velocidade e o diâmetro do próprio equipamento, temos:

\[ D=6,5 cm = 6,5.10^{-2} m \ \ \ \ \ (Eq.\ \ 52) \]

\[ v=11,12 m/s \ \ \ \ \ (Eq.\ \ 53) \]

Utilizando a Eq. 9:

\[ Q=A_{p}.v=\frac{\pi.D^{2}}{4}.v=0,03689 m^{3}/s \ \ \ \ \ (Eq.\ \ 54) \]

Sabendo agora a vazão volumétrica, é possível calcular todos os outros parâmetros de interesse, considerando que o ar irá entrar a 20°C e utilizando a Eq. 10 adaptada:

\[ \rho_{ar 20°C}=1,2041 Kg/m^{3} \ \ \ \ \ (Eq.\ \ 55) \]

\[ \dot{m}=\rho_{ar}.Q=0,04443 Kg/s \ \ \ \ \ (Eq.\ \ 56) \]

Calculando propriedades do ar durante o aquecimento

Nesta etapa, serão calculados as características do ar como fluido, e seus parâmetros, a resistência necessária para se atingir aquela temperatura de interesse e a temperatura de superfície durante o aquecimento. Para esta questão, será tratado como um caso de transferência de calor por convecção interna forçada, pois teremos a resistência acoplada ao tubo que irá sair do difusor até o aquecedor, e depois passará pelo bocal, para a mangueira. A resistência será utilizada após o soprador de ar, pois o escoamento antes da passagem nas pás tende a ser mais laminar e comportado, tendo um Reynolds menor e consequentemente um coeficiente de convecção (h) menor, tendo uma menor troca de calor. Colocando a resistência após passar do soprador de ar, por mais que a resistência deva ser mais potente devido aos efeitos convectivos, o escoamento é turbulento, ou quase turbulento, tendo um Reynolds maior, e consequentemente um coeficiente convectivo maior e maior troca de calor.

De acordo com o artigo de Rafael de Lima (Friedrich de Lima et al., 2015), a temperatura de aquecimento para o grão deve ser entre 60 a 80°C, e para este estudo será considerado 60°C e uma entrada de ar a 20°C. Primeiro, pode-se escrever a taxa de tranferência de calor pela eQ:

\[ \dot{Q}=h.A_s.\Delta T = c_p.\dot{m}.(T_s-T_e) \ \ \ \ \ (Eq.\ \ 57) \]

\[ \dot{Q}=1,004.0,067.(60-20)=1,48 kW \ \ \ \ \ (Eq.\ \ 58) \]

\[ P_{aquecedor}=\dot{Q}=1,48kW \ \ \ \ \ (Eq.\ \ 59) \]

Desta maneira, para alcançar um temperatura de 60°C do fluido, é necessário que a resistência utilizada forneça uma potência igual ou maior que 1480 Watts.

Agora será calculado o coeficiente convectivo a partir dos parâmetros e valores admensionais tratados anteriormente no tópico de "Transferência de Calor". Para começar, será calculada a temperatura média pela Eq. 43:

\[ T_m=\frac{T_{saida}+T_{\infty}}{2}=\frac{60-20}{2}=40°C \ \ \ \ \ (Eq.\ \ 60) \]

Olhando a tabela A-15 do livro do Çengel (A. Çengel; J. Ghajar, 2012), tem-se as seguintes propriedades do ar para 40°C:

\(\rho=1,127 Kg/m^{3}\\\) \(c_{p}=1,007 KJ/Kg.K\\\) \(K=0,02662 W/m.K\\\) \(\mu=1,918.10^{-5}Kg/m.s\\\) \(\upsilon=1,702.10^{-5}m^{2}/s\\\) \(Pr=0,7255\\\)

Calculando Reynolds utilizando (Eq. 27):

\[ Re=\frac{\rho.v.D}{\mu}=\frac{62,85.6,5.10^{2}}{1,918.10^{-5}}=0,983.10^{5} \]

Como descrito anteriormente, como \(0,983.10^{5}<5.10^{5}\), então este escoamento é caracterizado como um escoamento laminar. E desta maneira será utilizada a equação empírica (Eq. 44):

\[Nu=0,023.Re^{0,8}.Pr^{1/3}=203,851\]

E por fim, calculando o coeficiente de convecção pela (Eq. 42):

\[h=\frac{k.Nu}{D}=180,88378 W/m^{2}.K\]

Este valor poderá ser utilizado para melhorar as simulações termodinâmicas do silo.